加、减、乘、除是我们所熟悉的四则运算,定义新运算就是打破原有的运算规则,给出一种新的运算方法,并赋予该运算方法新的运算符号,如*、△、◎、※等。
示例:若a△b=a+b+ab,求3△2?
解答这类题目的关键是理解新定义,严格按照新定义的式子代入数值,把定义的新运算转化成我们所熟悉的四则运算。对上题,有 3△2=3+2+3×2=11。
一、解题注意事项
(1)无特殊规定时,按从左到右的顺序计算;有括号时,应当先算括号里面的。
(2)新定义的运算往往不一定具备交换律和结合律,不能随便套用这些运算律来解题。
(3)如※,△,●,★等符号所表示的运算并不是一种固定的算法,而是因题而异,不同的题目有不同的规定,我们应当严格按不同的规定进行运算。
例题:对于数x、y规定运算“○”为x○y=(x+4)×(y-3)。则7○(8○9)的值为( )。
A.300 B.429 C.672 D.759
解析:此题答案为D。有括号,先算括号里的。
8○9=(8+4)×(9-3)=72。
原式=7○72=(7+4)×(72-3)=759,即7○(8○9)=759。
二、定义新运算常见考点精讲
1.根据新定义直接计算
例题:定义新运算:对于任意自然数A、B,若A、B奇偶性相同,则A※B=
(A+B)÷2;若A、B奇偶性不同,则A※B=(A+B+1)÷2。那么1※3※5=( )。
A.2 B.4 C.8 D.12
解析:此题答案为B。题中没有给出三个数以两个※相连的计算公式,但是与加法、乘法等运算类比,可知应该从左到右顺次计算。
先求出1※3的值,1和3同是奇数,1※3=(1+3)÷2=2;
再根据公式来求2※5的数值,2和5奇偶性不同,2※5=(2+5+1)÷2=4。
所以1※3※5=2※5=4。
2.解未知数
定义新运算后,算式中有未知数,要求由结果求解未知数。解题时,专家认为按照新定义代入已知数字和未知数,再根据已掌握的方程解法解方程。
例题1:对于a,b,c,d,规定=2ab-c+d。如果,<1,3,5,x>=7,那么x=( )。
A.3 B.6 C.8 D.9
解析:此题答案为B。按照新定义,<1,3,5,x>=2×1×3-5+x=1+x,所以1+x=7,解得x=6。

3.先确定规律再代入计算
这类问题中,新定义的规律并不直接给出,而是通过几个算式,需要考生通过算式自己寻找出其中的规律,再代入计算。
例题:定义4△5=4+5+6+7+8=30,7△4=7+8+9+10=34,按此规律,(26△15)+(10△3)的值为()。
A.528 B.525 C.423 D.420
解析:此题答案为A。没有直接给出规律,需要先确定规律。
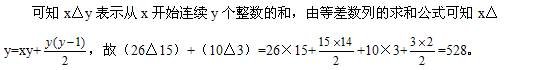
【跟踪小练习】:
1.定义新运算:3△2=3+33=36,2△3=2+22+222=246,1△4=1+11+111+1111=1234。则8△6的值为:
A.886728 B.986720 C.986725 D.987648
2.已知x、y满足x+[y]=2009,{x}+y=20.09;其中[x]表示不大于x的最大整数,{x}表示x的小数部分,即{x}=x-[x],那么x=( )。
A.2009 B.2008 C.1999 D.1989
3.对于任意的两个自然数a和b,规定新运算*:a*b=a(a+1)(a+2)…(a+b-1),其中a、b表示自然数。如果(x*3)*2=3660,那么x等于几?
A.3 B.4 C.5 D.6
【参考答案及解析】:
1.【答案】D。解析:依题意,8△6=8+88+888+8888+88888+888888=987648。本题可以用尾数法,个位数有6个8,所以尾数为8,排除B、C。又因为该结果肯定大于888888,所以排除A,选择D。
2.【答案】D。解析:根据题意,[y]是整数,所以x=2009-[y]也是整数,即[x]=x,那么{x}=x-[x]=0,由此可得y=20.09-{x}=20.09-0=20.09,所以[y]=20,x=2009-[y]=2009-20=1989。
3.【答案】A。解析:由题中所给定义可知,b为多少,则就有多少个乘数。3660=60×61,即60*2=3660,则x*3=60;而60=3×4×5,即3*3=60,所以x=3。
行测更多解题思路和解题技巧,可参看2012年公务员考试技巧手册。


