1.乘除法转化法公式

　　2.乘除法转化法适用情形

　　计算某一分式的具体数值时，如果除数的形式为（1+x），其中│x│＜10%，且选项间的差距大于绝对误差时，那么可以使用乘除法转化法，将除法转化为乘法从而降低计算难度。

　　3.绝对误差与相对误差

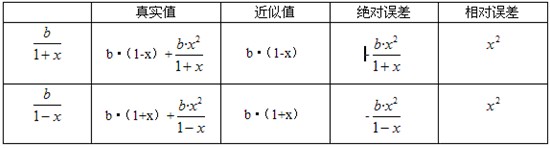
　　在计算过程中，可以用-b·x2近似估算一下绝对误差值，当选项间的差距大于绝对误差值时，可以使用该方法进行转化计算。

　　例题1： 3772÷（1+3.4%）=（    ）。

　　A.3905             B.3648

　　C.3678             D.3702

　　解析：此题答案为B。由于1+3.4%>1，所以3772÷（1+3.4%）<3772，排除A项；应用乘除法转化法3772÷（1+3.4%）≈3772×（1-3.4%）≈3772-3772×3%-3772×0.4%≈3772-111-12=3649，最接近的是B项。

　　误差分析：3772÷（1+3.4%）的相对误差为（3.4%）2 =0.001，按照乘除法转化法计算绝对误差的公式，该算式的绝对误差估算为-3772×（3.4%）2 =-4.4，小于选项间的差距，因此可以用乘除法转化法进行估算。

　　例题2：

　　2002年我国的粮食产量约为（    ）。

　　A．45722万吨  B．44965万吨  C．44761万吨  D．40709万吨

　　解析：此题答案为A。由图可知，2003年全国粮食产量为43070万吨，增长率为-5.8%，则2002年全国粮食产量为43070÷（1-5.8%）≈43070×（1+5.8%）≈43070+43070×6%-43070×0.2%≈43070+2580-90=45560万吨，即可得到A项。

　　行测更多解题思路和解题技巧，可参看2013年公务员考试技巧手册。