一、时针法
时针法是较为简单的一种方法,无非是以立体图形中相邻的三个面为基准,分别去选项中找寻这三个面,并按照同样的顺序画时针。然而并非任意三个面都可以画时针,在六面体中,能够画时针的三个面必须满足以下两个条件:
(1)画时针的三个面必须不存在平行面;
(2)画时针的时候必须保证这三个面至少两对两两有交点。二者缺一不可。如在下图中,两个平面图中1、2、3三个面都不平行,这满足了画时针的第一个条件;第一个图形中1、2两个面有交点,即两个红点,2、3两个面也有交点,即一个蓝点,第二个图形中1、2两个面的交点为a、b,1、3两个面的交点为b、c,2、3两个面的交点为b,第一个图形中两对面两两有交点,第二个图形中三对面都两两有交点,所以满足画时针的第二个条件,很明显,这两个图是可以直接画时针的。
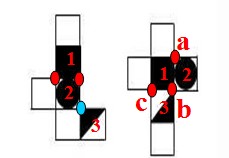
但是,在有些空间重构类的题目中,是并不满足直接画时针的条件的。如:下图中的1点、3点、6点三个面,虽然三个面都不平行,但是很明显只有1点、3点之间有公共点,但是6点和它们并没有公共点,所以不满足画时针的条件(2),此时要移动,根据平行面来移动,6点和2点平行,所以可以将6点移动到红字标出的1和2的位置,无论是1的位置还是2的位置都可以直接画时针了。
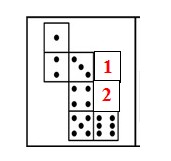
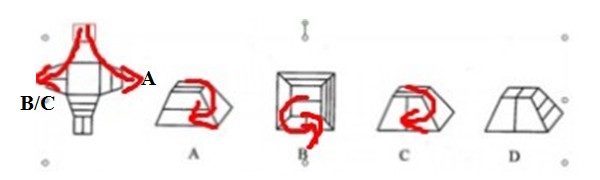
另外,在非正六面体中,时针法也完全适用,而且不论是内表面还是外表面,因为在平面图形中,内外皆可。如下题。A选项中的三个面在原图中找到后,发现不满足画时针的第2个条件,所以将类似立体容器盖子的最小正方形移到了上方,右边的逆时针为A选项在平面中的时针,与A立体图中的顺时针不一致,所以A错,同理可知C对。
下图给定的是纸盒的外表面,下面哪一项能由它折叠而成?
二、公共顶点法
此处的知识点有三条:
(1)互相垂直的两条边(必须是长度一样的边)的端点是公共顶点;
(2)对面/平行面之间不可能有公共顶点;
(3)相交于同一个公共顶点下的三个面,其面上的图形必须与公共顶点的位置关系保持不变。
第(1)点有老师教研过,此处不再赘述,即下图中三个红点、三个蓝点折成立体图形后会是同一个公共顶点。第(2)点理解起来容易,但用起来难度较大。如何来用,如下图:两个粉色的点a、b是公共顶点。原因如下:a在1面和3面上就不可在1面和3面的平行面上即5和6面,而1、3、4的公共点也很显然,所以相交于a点的另一个面肯定是2面,而2面上的红点不可能,2面下方的两个点因为在6面上,自然也不能在其平行面3面上,所以也排除,只能是b点。
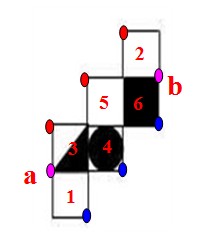
第(3)点用起来较简单,也比较常用,但要基于(1)和(2)两点即在找到公共顶点的情况下。如下面例题:
其中红点是A选项中的公共顶点,原图中1面上的斜线未经过公共点,而A选项经过了,所以错了;黑点是B选项中的公共顶点。原图中2面上的斜线未经过公共顶点,但B选项经过了,所以错了;C选项用公共顶点无法直接看出,可以用时针法排除,但要确定C选项中2、3这两个面也是有一定难度的,完全可以按照公共顶点,发现3面中红色线段标示的地方,相应的找到2和3面,直接用时针就可以。
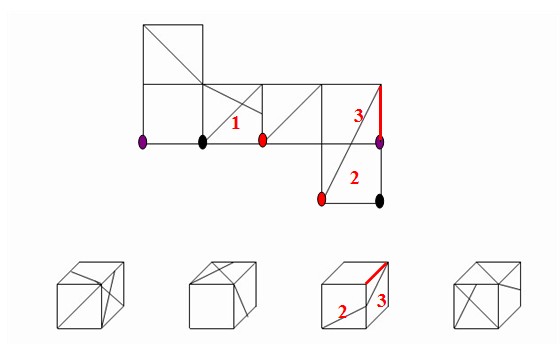
公共顶点法在类似此题这种带有斜线等明显图形特征的题目是特别好用,结合时针法,即快速又高效。
行测更多解题思路和解题技巧,可参看2013年公务员考试技巧手册。


